Answer:
the pH of HCOOH solution is 2.33
Step-by-step explanation:
The ionization equation for the given acid is written as:
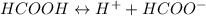
Let's say the initial concentration of the acid is c and the change in concentration x.
Then, equilibrium concentration of acid = (c-x)
and the equilibrium concentration for each of the product would be x
Equilibrium expression for the above equation would be:
![\Ka= ([H^+][HCOO^-])/([HCOOH])](https://img.qammunity.org/2021/formulas/chemistry/college/t7ki421vup5zmap97i860hhh80xljovdzs.png)
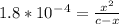
From given info, equilibrium concentration of the acid is 0.12
So, (c-x) = 0.12
hence,

Let's solve this for x. Multiply both sides by 0.12
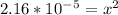
taking square root to both sides:
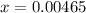
Now, we have got the concentration of
![[H^+] .](https://img.qammunity.org/2021/formulas/chemistry/college/zchvm4depbnghe32llhwghwfv4il2vmwiw.png)
![[H^+] = 0.00465 M](https://img.qammunity.org/2021/formulas/chemistry/college/dpa2g1lzbnx112pbuwqhxcyc1malgxtfqk.png)
We know that,
![pH=-log[H^+]](https://img.qammunity.org/2021/formulas/chemistry/college/wyj0nahkywle04sx44478osqilvygxax2t.png)
pH = -log(0.00465)
pH = 2.33
Hence, the pH of HCOOH solution is 2.33.