Answer:
90% confidence interval for the true proportion of air travelers who prefer the window seat is (0.575, 0.625)
Explanation:
We have the following data:
Sample size = n = 1000
Proportion of travelers who prefer window seat = p = 60%
Standard Error = SE = 0.015
We need to construct a 90% confidence interval for the proportion of travelers who prefer window seat. Therefore, we will use One-sample z test about population proportion for constructing the confidence interval. The formula to calculate the confidence interval is:
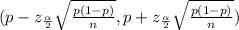
Since, standard error is calculated as:
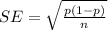
Re-writing the formula of confidence interval:
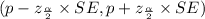
Here,
 is the critical value for 90% confidence interval. From the z-table this value comes out to be 1.645.
is the critical value for 90% confidence interval. From the z-table this value comes out to be 1.645.
Substituting all the values in the formula gives us:
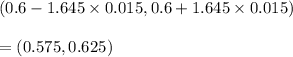
Therefore, the 90% confidence interval for the true proportion of air travelers who prefer the window seat is (0.575, 0.625)