Question

The mean of the sample is 24.444 squares with a standard deviation of 2.45 squares. Single-ply toilet paper requires 26 squares to absorb one-quarter cup of water. Josh would like to carry out a test to determine if there is convincing evidence that the mean number of squares of Fluffy that are needed to absorb one-quarter cup of water is fewer than 26 squares. What is the appropriate test statistic and P-value of this test?

Answer 1

t = -2.69 , p = 0.0078

Explanation:

We have the following data:

Sample Mean = x = 24.444

Sample Standard Deviation = s = 2.45

Sample size = n = 18

Josh wants to test that mean number is lesser than 26. So our test value is 26 i.e.

u = 26

Since Josh wants to test that mean would be fewer than 26, so this would be a left tailed test with a less than sign in Alternate Hypothesis. Therefore, the hypothesis would be:

`H_(o): u\geq 26\\H_(a): u<26`

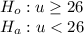
Since, we do not know the value of Population standard deviation, and we have the value of sample standard deviation, we will use One-Sample t-test for the population mean.

The formula to calculate the test-statistic would be:

`t=(x-u)/((s)/(√(n)))`

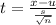
Substituting the values in this formula gives us:

`t=(24.444-26)/((2.45)/(√(18)))\\t=-2.69`

This means, the test statistic would be -2.69

Since, the sample size is 18, the degrees of freedom would be:

Degrees of freedom = df = n - 1 = 17

To find the p-value we need to check the p-value against test statistic of 2.69, with 17 degrees of freedom and One-tailed test. This value comes out to be:

p-value = 0.0078

Therefore, the correct answer would be:

t = -2.69 , p = 0.0078