Answer:

Explanation:
a. This is a binomial probability distribution problem expressed as:
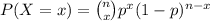
Where:
 is the probability a successful event.
is the probability a successful event.
 the number of successful events.
the number of successful events.
 is the total number of events.
is the total number of events.
Given n=10, p=0.47 the probability of exactly 5 is calculated as:
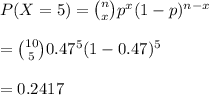
Hence, the probability that exactly 5 adults have very little confidence is 0.2417
b. Given n=10, p=0.47,
-We substitute our values in formula and the probability of at least 6 is calculated as:

Hence, the probability of at least 6 adults is 0.3056
c. The probability of of less that four adults is calculated as:

Hence, the probability that less that 4 adults have confidence in the newspapers is 0.2255