Question

According to a study conducted by an​ organization, the proportion of Americans who were afraid to fly in 2006 was 0.10. A random sample of 1 comma 100 Americans results in 121 indicating that they are afraid to fly. Explain why this is not necessarily evidence that the proportion of Americans who are afraid to fly has increased.

Answer 1

Event is not unusual(p>0.05).

Explanation:

Given that :

`p=0.10\\\\n=1100\\\\x=121`

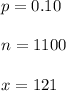
#The sample proportion is calculated as:

`\hat p=(x)/(n)\\\\=(121)/(1100)\\\\=0.1100`

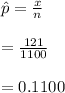
#Mathematically, the z-value is the value decreased by the mean then divided the standard deviation :

`z=\frac{\hat p- p}{\sqrt{(p(1-p))/(n)}}\\\\\\\\=\frac{0.11-0.10}{\sqrt{(0.10(1-0.10))/(1100)}}\\\\\\=1.1055`

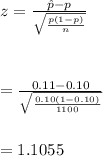
#We use the normal probability table to determine the corresponding probability;

`P(X\geq 121)=P(Z>1.1055)\\\\=0.1314`

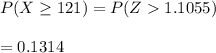
Hence, the probaility is more than 0.05, thus the event not unusual and thus this is not necessarily evidence that the proportion of Americans who are afraid to fly has increased.