Answer:
The fraction increase by (
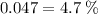 ) if its numerator is
) if its numerator is
increased by 25% and its denominator is increased by 20%.
Explanation:
- Let 'd' be the denominator
As
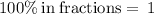
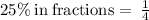
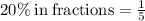
so
Increase in 25% means
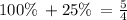
Increase in 20% means
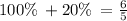
Thus the fraction becomes
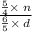
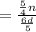
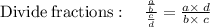
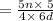
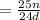
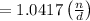
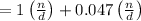
As
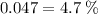
Therefore, the fraction increase by (
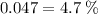 ) if its numerator is
) if its numerator is
increased by 25% and its denominator is increased by 20%.