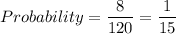Answer:
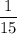
Step-by-step explanation:
The number of different ways in which the two armadillos would be at the ends of the row is 2:
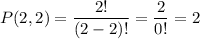
The number of different combinations in which two of the three aardvarks can sit at the ends of the row is P(3,2):
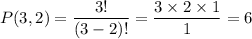
Therefore, there are 2 + 6 = 8 different ways in which the two animlas on the ends of the row were both armadillos or both aardvarks.
Now calculate the total number of different ways in which the animals can sit. It is P(5,5):

Thus, the probability that the two animals on the ends of the row were both armadillos or both aardvarks is equal to the number of favorable outputs divided by the total number of possible outputs: