Question

QUESTION 16 The body temperatures of adults have a mean of 98.6° F and a standard deviation of 0.60° F. If 36 adults are randomly selected, find the probability that their mean body temperature is greater than 98.5° F. Hint: You will need to use the sampling distribution of the sample mean.

Answer 1

34%

Explanation:

The body temperatures of adults have a mean of 98.6° F and a standard deviation of 0.60° F.

We want to find the probability that the mean body temperature of 36 randomly selected adults is greater than 98.5° F.

The mean of the sampling distribution of the sample means is the same as the population mean,

`\mu = 98.6 \degree`

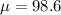
The standard error of the mean becomes the standard deviation of the sampling distribution of the means.

`SE= ( \sigma)/( √(n) )`

`SE= (0.6)/( √(36) ) = 0.1`

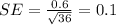
By the Central Limit Theorem, the distribution of mean of means is approximately normal

The z-score of 98.5° F

`z= (98.5 - 98.6)/(0.1) = - 1`

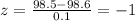
By the empirical rule 68% of the distribution is within one standard deviation (-1 to 1).

Therefore from (-1 to 0), it will be approximately 34%