Question

At a certain university, 22% of the students fail general chemistry on their first attempt. Professor Brown teacher at this university and believes that the rate of first-time failure in his general chemistry classes is 45%. He samples 86 students from last semester who were first-time enrollees in general chemistry and finds that 19 of them failed his course.

1) State the appropriate null and alternate hypotheses.
2) Compute the P-value.
3) Using a = 0.05, can Professor Brown conclude that the percentage of failures differs from 45%?

Answer 1

`a. \ H_o:p=0.45, \ \ \ \ H_a:p\\eq 0.45\\\\b.\ \hat p=0.2209\\\\c. \ Yes\ (-4.2706<-1.96)`

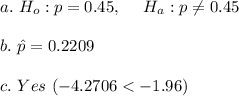
Explanation:

a. The professor's claim is that 45% first-timers fail his test. The null hypothesis is therefore stated as:

`H_o:p=0.45`

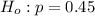
-The alternative hypothesis is that more or less people fail the test as opposed to the professor's exact claim, hence:

`H_a:p\\eq 0.45`

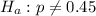
b. To compute the P-value we use the z-value for a 95% confidence level:

`z_(\alpha/2)=z_(0.025)=1.96`

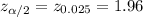
#The proportion of failures in the sample of 86 is 19:

`\hat p=(19)/(86)\\\\=0.2209`

The z-value is calculated as:

`z=\frac{\hat p-p_o}{\sqrt{(p_o(1-p_o))/(n)}}`

`=\frac{0.2209-0.45}{\sqrt{(0.45(1-0.45))/(86)}}\\\\\\=-4.2706`

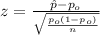
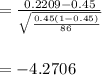
-4.2706 is less than the stated confidence level for the given 45% proportion and greatly differs from it.

- Reject the null hypothesis as there is enough evidence to reject the claim.

-Hence,Yes, Professor Brown can conclude that percentage of failures differs from 45%.