Answer:
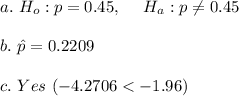
Explanation:
a. The professor's claim is that 45% first-timers fail his test. The null hypothesis is therefore stated as:
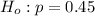
-The alternative hypothesis is that more or less people fail the test as opposed to the professor's exact claim, hence:
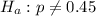
b. To compute the P-value we use the z-value for a 95% confidence level:

#The proportion of failures in the sample of 86 is 19:
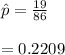
The z-value is calculated as:

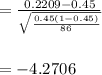
-4.2706 is less than the stated confidence level for the given 45% proportion and greatly differs from it.
- Reject the null hypothesis as there is enough evidence to reject the claim.
-Hence,Yes, Professor Brown can conclude that percentage of failures differs from 45%.