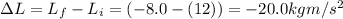Question

A spinning wheel has a rotational inertia of 2 kg•m². It has an angular velocity of 6.0 rad/s. An average counterclockwise torque of 5.0 N•m is applied, and continues for 4.0 s. What is the change in angular momentum of the wheel?

Answer 1

`-20.0 kg m^2/s`

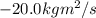
Step-by-step explanation:

The angular momentum of an object in rotation is given by

`L=I \omega`

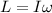
where

I is the moment of inertia

`\omega` is the angular speed

In this problem, initially we have

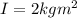`I=2 kg m^2` is the moment of inertia of the wheel

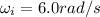`\omega_i = 6.0 rad/s` is the initial angular speed

So the initial angular momentum is

`L_i = I\omega_i = (2)(6.0)=12 kg m^2/s`

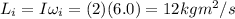
Later, a counterclockwise torque of

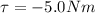`\tau=-5.0 Nm` is applied

So the angular acceleration of the wheel is:

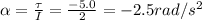`\alpha = (\tau)/(I)=(-5.0)/(2)=-2.5 rad/s^2` in the direction opposite to the initial rotation.

As a result, the final angular velocity of the wheel will be:

`\omega_f = \omega_i + \alpha t`

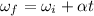
where

t = 4.0 is the time interval

Solving,

`\omega_f = +6.0 +(-2.5)(4.0)=-4 rad/s`

which means that now the wheel is rotating in the counterclockwise direction.

Therefore, the new angular momentum of the wheel is:

`L_f = I\omega_f =(2)(-4.0)=-8.0 kg m^2/s`

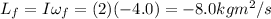
So, the change in angular momentum is:

`\Delta L=L_f - L_i = (-8.0-(12))=-20.0 kg m/s^2`