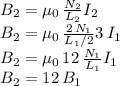Answer:
the field at the center of solenoid 2 is 12 times the field at the center of solenoid 1.
Step-by-step explanation:
Recall that the field inside a solenoid of length L, N turns, and a circulating current I, is given by the formula:

Then, if we assign the subindex "1" to the quantities that define the magnetic field (
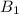 ) inside solenoid 1, we have:
) inside solenoid 1, we have:

notice that there is no dependence on the diameter of the solenoid for this formula.
Now, if we write a similar formula for solenoid 2, given that it has :
1) half the length of solenoid 1 . Then
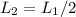
2) twice as many turns as solenoid 1. Then
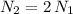
3) three times the current of solenoid 1. Then
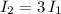
we obtain: