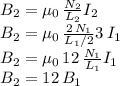Question

We have two solenoids: solenoid 2 has twice the diameter, half the length, and twice as many turns as solenoid 1. The current in solenoid 2 is three times that in solenoid 1. How does the field B2 at the center of solenoid 2 compare to B1 at the center of solenoid 1?

Answer 1

the field at the center of solenoid 2 is 12 times the field at the center of solenoid 1.

Step-by-step explanation:

Recall that the field inside a solenoid of length L, N turns, and a circulating current I, is given by the formula:

`B=\mu_0\, (N)/(L) I`

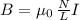
Then, if we assign the subindex "1" to the quantities that define the magnetic field (
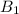`B_1`) inside solenoid 1, we have:

`B_1=\mu_0\, (N_1)/(L_1) I_1`

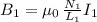
notice that there is no dependence on the diameter of the solenoid for this formula.

Now, if we write a similar formula for solenoid 2, given that it has :

1) half the length of solenoid 1 . Then
`L_2=L_1/2`

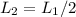
2) twice as many turns as solenoid 1. Then
`N_2=2\,N_1`

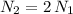
3) three times the current of solenoid 1. Then
`I_2=3\,I_1`

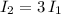
we obtain:

`B_2=\mu_0\, (N_2)/(L_2) I_2\\B_2=\mu_0\, (2\,N_1)/(L_1/2) 3\,I_1\\B_2=\mu_0\, 12\,(N_1)/(L_1) I_1\\B_2=12\,B_1`