Answer:
144 feet
Explanation:
The quadratic equation is:
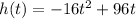
The general form of a quadratic is
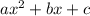
So, we can match the equations and say:
a = -16
b = 96
c = 0
Now, for quadratic equations, the max value occurs at
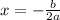 and the max value is what we get when we put that number in the function. First, lets find the value on which is occurs:
and the max value is what we get when we put that number in the function. First, lets find the value on which is occurs:
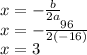
Now, put x = 3 into the equation:
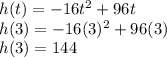
The max height of projectile is 144 feet