Question

She Elle has 100 meters of fencing to build a rectangular garden. The garden's area (in square meters) as a function of the garden's width "w" (in meters) is modeled by: A(w) = -(w-25)^2+625 What is the maximum area possible in square meters?

Answer 1

Explanation:

Answer 2

`625 m^2`

Explanation:

In this problem, we are told that the area of the garden is given by the expression

`A(w)=-(w-25)^2+625`

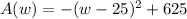
where

w is the width of the garden (in meters)

Here we want to find the maximum possible area.

The maximum of a function f(x) can be found by requiring that its first derivative is zero:

`f'(x)=0`

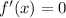
Therefore, here we have to calculate the derivative of
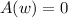`A(w)=0` and find the value of w for which it is equal to zero.

Let's start by rewriting the area function as

`A(w)=-(w^2-50w+625)+625=-w^2+50w`

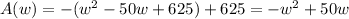
Now we calculate the derivative with respect to w:

`A'(w)=-2w+50`

Now we require this derivative to be zero, so

`-2w+50=0\\w=-(50)/(-2)=25 m`

So now we can substitute this value of w into the expression of A(w) to find the maximum possible area:

`A(25)=-(25-25)^2+625 = 625 m^2`

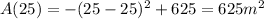
This value is allowed because we know that the maximum length of the perimeter of the fence is 100 meters; If the garden has a square shape, the length of each side is
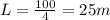`L=(100)/(4)=25 m`, and the area of the squared garden is

`A=L^2=(25)^2=625 m^2`

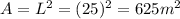
Which is equal to what we found earlier: this means that the maximum area is achieved if the garden has a squared shape.