Question

Question in the picture:)

Answer 1

Given:

Set A represents rational numbers.

Set B represents integers.

Set C represents whole numbers.

To find:

Which of the value represents a value that could be placed in set C.

Solution:

Rational number is ratio of two numbers which of the form
`(p)/(q), \ q\\eq0`.

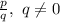Integer is a set of positive and negative numbers including zero.

Integers: {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}

Whole numbers are positive numbers with zero.

Whole numbers: {0, 1, 2, 3, 4, ...}

Option A: -10

-10 is a integer. So that, it is placed in set B not in set C.

Therefore, it is not true.

Option B: 2.5

2.5 can be written as
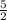`(5)/(2)`. It is a rational number.

Rational number placed in set A.

Therefore, it is not true.

Option C:
`(1)/(4)`

`(1)/(4)` is a rational number.

Rational number placed in set A.

Therefore, it is not true.

Option D:
`(12)/(4)`

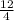
`$(12)/(4)=3` (cancelling common factors)

3 is a whole number.

Whole numbers placed in set C.

Therefore, it is true.

Hence
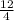`(12)/(4)` is the value that could be placed in set C.