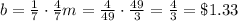Question

Bella spent 4/7 of her money on a dictionary and 3 identical books. She spent 1/6 of the remainder on a journal that cost $7. a) How much did she spend on the dictionary and 3 books? b) If 3/8 of the cost of the dictionary was the same as 1/2 of the total cost of 3 books, how much did each book cost?

Answer 1

a) 9.33$

b) 1.33$

Explanation:

a)

To solve the problem, let's call

`m` = the money that Bella has at the beginning

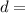`d=` the price of a dictionary

`b=` the price of one book

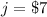`j=\$7` the price of the journal

Here, Bella spent 4/7 of her money to buy a dictionary and 3 books, so

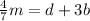`(4)/(7)m=d+3b` (1)

Then she spent 1/6 of the remainder (which is
`(3)/(7)m`) to buy the journal so

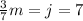`(3)/(7)m=j=7` (2)

So from this second equation we can find m, the money that she has at the beginning:

`m=(7)/(3)\cdot 7 =(49)/(3)=\$16.3`

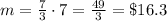
So the amount that she spent for the dictionary + the 3 books is

`(4)/(7)m = (4)/(7)\cdot (49)/(3)=(28)/(3)=\$9.33`

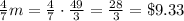
b)

Here, we are told that

3/8 of the cost of the dictionary was the same as 1/2 of the total cost of 3 books

Which can be rewritten as an equation as follows:

`(3)/(8)d=(1)/(2)(3b)`

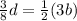
This means that we can rewrite the cost of the dictionary by re-arranging this equation as:

`d=(8)/(3)\cdot (1)/(2)(3b) =4b`

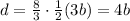
Substituting into eq.(1) of part a),

`(4)/(7)m=4b+3b\\(4)/(7)m=7b`

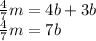
And from this, we can find b, the cost of each book:

`b=(1)/(7)\cdot (4)/(7)m=(4)/(49)\cdot (49)/(3)=(4)/(3)=\$1.33`