Answer:
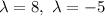
Explanation:
Eigenvalues of a Matrix
Given a matrix A, the eigenvalues of A, called
 are scalars who comply with the relation:
are scalars who comply with the relation:
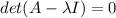
Where I is the identity matrix
![I=\left[\begin{array}{cc}1&0\\0&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/cjdeue4d9yfys4q5yc12xdtadj1nddzh4n.png)
The matrix is given as
![A=\left[\begin{array}{cc}3&5\\8&0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/8jypexd2jhr8jv7zqrcxlfls8hztz0mfkd.png)
Set up the equation to solve
![det\left(\left[\begin{array}{cc}3&5\\8&0\end{array}\right]-\left[\begin{array}{cc}\lambda&0\\0&\lambda \end{array}\right]\right)=0](https://img.qammunity.org/2021/formulas/mathematics/college/91dg6wr35ks9exf16ua5ijlz2glsptp3lo.png)
Expanding the determinant
![det\left(\left[\begin{array}{cc}3-\lambda&5\\8&-\lambda\end{array}\right]\right)=0](https://img.qammunity.org/2021/formulas/mathematics/college/j4biyawj9aq6tpvg88zl603c3hba0tsees.png)

Operating Rearranging
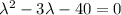
Factoring
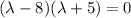
Solving, we have the eigenvalues
