Question

Consider the graph that represents the following quadratic equation.

y=-1/3(x+2)^2+5
--the graph opens:
-downward
-upward
--the vertex of the graph is:
-(2,5)
-(-2,-5)
-(-2,5)
--the axis of symmetry of the graph is:
-x=2
-x=-2

Answer 1

Part 1) The graphs open downward

Part 2) The vertex is the point (-2,5)

Part 3) The axis of symmetry is x=-2

Explanation:

step 1

we have

`y=-(1)/(3)(x+2)^2+5`

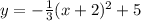
This is a vertical parabola open downward (because the leading coefficient is negative)

The vertex is a maximum

step 2

The quadratic equation is written in vertex form

`y=a(x-h)^2+k`

where

(h,k) is the vertex

so

In this problem

The vertex is the point (-2,5)

step 3

The equation of the axis of symmetry of a vertical parabola is equal to the x-coordinate of the vertex

The x-coordinate of the vertex is -2

therefore

The axis of symmetry is x=-2