Question

HELPPPP!!!!
Need the answer ASAP!!

Answer 1

Given that the functions
`f(x)=x+4` and
`g(x)=x^(3)`

We need to determine the value of the function
`(g \ {\circ} f)(-3)`

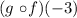
First, we shall determine the composition of the function
`(g \circ f)(x)`

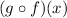
Function
`(g \circ f)(x)`:

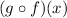Let us determine the function
`(g \circ f)(x)`

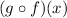
Thus, we have;

`(g \circ f)(x)=g[f(x)]`

`=g[x+4]`

`=(x+4)^3`

`(g \circ f)(x)=x^3+3x^2(4)+3x(4)^2+(4)^3`

`(g \circ f)(x)=x^3+12x^2+48x+64`

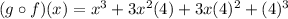
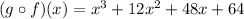
Thus, the function is
`(g \circ f)(x)=x^3+12x^2+48x+64`

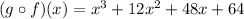
Value of the function
`(g \ {\circ} f)(-3)`:

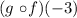The value of the function can be determined by substituting x = -3 in the function
`(g \circ f)(x)=x^3+12x^2+48x+64`

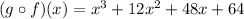
Thus, we have;

`(g \circ f)(-3)=(-3)^3+12(-3)^2+48(-3)+64`

Simplifying the terms, we get;

`(g \circ f)(-3)=-27+12(9)+48(-3)+64`

`(g \circ f)(-3)=-27+108-144+64`

`(g \circ f)(-3)=1`

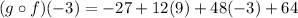
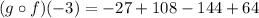
Thus, the value of the function
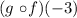`(g \ {\circ} f)(-3)` is 1.