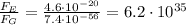Question

a proton is placed 100 micrometers from a helium nucleus. Gravity pulls the proton and nucleus together, while the electric force pushes them apart. Which is stronger, and by how much?

Answer 1

The electric force is
`6.2\cdot 10^(35)` times stronger than the gravitational force

Step-by-step explanation:

The magnitude of the electrostatic force between two charges is given by:

`F_E=k(q_1 q_2)/(r^2)`

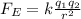
where:

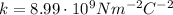`k=8.99\cdot 10^9 Nm^(-2)C^(-2)` is the Coulomb's constant

`q_1, q_2` are the two charges

r is the separation between the two charges

In this problem:

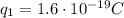`q_1=1.6\cdot 10^(-19)C` (charge of the proton)

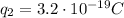`q_2=3.2\cdot 10^(-19)C` (charge of a nucleus of helium, twice the charge of a proton)

`r=100 \mu m = 100\cdot 10^(-6) m`

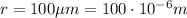
So the electric force is

`F_E=(8.99\cdot 10^9)((1.6\cdot 10^(-19))(3.2\cdot 10^(-19)))/((100\cdot 10^(-6))^2)=4.6\cdot 10^(-20) N`

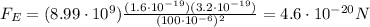
Instead, the magnitude of the gravitational force between two objects is given by :

`F_G=G(m_1 m_2)/(r^2)`

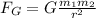
where

`G=6.67\cdot 10^(-11) m^3 kg^(-1)s^(-2)` is the gravitational constant

m1, m2 are the masses of the two objects

r is the separation between them

Here we have:

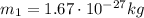`m_1=1.67\cdot 10^(-27)kg` is the mass of the proton

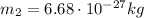`m_2=6.68\cdot 10^(-27)kg` is the mass of a nucleus of helium (4 times the mass of the proton)

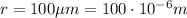`r=100 \mu m = 100\cdot 10^(-6) m` is the separation

So the gravitational force is

`F_G=(6.67\cdot 10^(-11))((1.67\cdot 10^(-27))(6.68\cdot 10^(-27)))/((100\cdot 10^(-6))^2)=7.4\cdot 10^(-56) N`

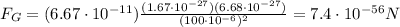
So, we see that the electric force is much stronger than the gravitational factor, by a factor of:

`(F_E)/(F_G)=(4.6\cdot 10^(-20))/(7.4\cdot 10^(-56))=6.2\cdot 10^(35)`