Answer:
C.
Explanation:
In trigonometry, we have an equation as following:
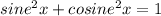
Replace θ into the above equation, we would have:
(sine θ)^2 + (cosine θ)^2 = 1
=> (sine θ)^2 = 1 - (cosine θ)^2 (1)
As given, we have cosine θ = -3/7. Replace it into the equation (1), we have:
(sine θ)^2 = 1 - (-3/7)^2
=>(sine θ)^2 = 1 - 9/49 = 40/49
=> sine θ = ±
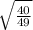 = ±
= ±

So sine θ =
 or sine θ = -
or sine θ = -

However, as θ is in quadrant II, sine θ has a positive value
=> sine θ =

So that the correct answer is C