Answer:
the factor of safety is 3.87
Step-by-step explanation:
Outside diameter, d₀ = 3.5 in
Thickness, t = 0.065 in
Poission ratio, v = 0.334
Yield strength,
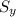 = 46 kpsi = 46000 psi
= 46 kpsi = 46000 psi
Pressure release load, d₁ = d₀ - 2t = 3.5 - (2 x 0.065) = 3.37 in
Tangential stress, σ₁ = P(d₁ + t) / 2t
= 500 (3.37 + 0.065) / 2 x 0.065
= 13211.5385 psi
σ₁ = P(d₁) / 4t = 500(3.37) / 4 x 0.065 = 6480.769 psi
Radial stress, σ₀ = -P ==> -500 psi
Principal stresses, σ' =
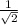 √[(σ₁ - σ₁)² + (σ₁ - σ₁)² + (σ₁ - σ₁)²]
√[(σ₁ - σ₁)² + (σ₁ - σ₁)² + (σ₁ - σ₁)²]
σ' =
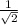 √[(13211.5385 - 6480.769)² + (6480.769 - (-500))² + (-500 - 13211.5385)²]
√[(13211.5385 - 6480.769)² + (6480.769 - (-500))² + (-500 - 13211.5385)²]
=11875.1986 psi
Factor of safety Л =
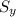 / σ'
/ σ'
= 46000 / 11875.1986
= 3.8736
Л = 3.87