Solution to equation
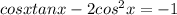 for all real values of x is
for all real values of x is
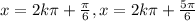 .
.
Explanation:
Here we have ,
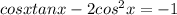 . Let's solve :
. Let's solve :
⇒
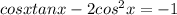
⇒
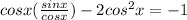
⇒
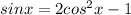
⇒
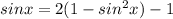
⇒
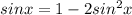
⇒
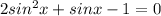
By quadratic formula :
⇒
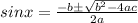
⇒
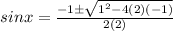
⇒
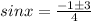
⇒
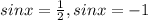
⇒
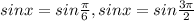
⇒

But at
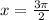 we have equation undefined as
we have equation undefined as
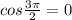 . Hence only solution is :
. Hence only solution is :
⇒
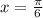
Since ,
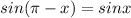
⇒
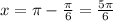
Now , General Solution is given by :
⇒
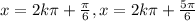
Therefore , Solution to equation
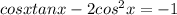 for all real values of x is
for all real values of x is
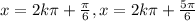 .
.