Question

Solve the equation for all real values of x.
cosxtanx - 2 cos^2 x=-1

Answer 1

Answer: B on edge

Explanation:

Answer 2

Solution to equation
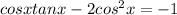`cosxtanx - 2 cos^2 x=-1` for all real values of x is
`x=2k\pi + (\pi)/(6) , x=2k\pi + (5\pi)/(6)` .

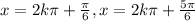Explanation:

Here we have ,
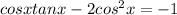`cosxtanx - 2 cos^2 x=-1`. Let's solve :

⇒
`cosxtanx - 2 cos^2 x=-1`

⇒
`cosx((sinx)/(cosx)) - 2 cos^2 x=-1`

⇒
`sinx = 2 cos^2 x-1`

⇒
`sinx = 2 (1-sin^2x)-1`

⇒
`sinx = 1-2sin^2x`

⇒
`2sin^2x+sinx-1=0`

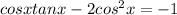
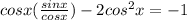
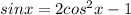
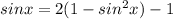
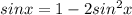
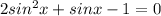
By quadratic formula :

⇒
`sinx = (-b \pm √(b^2-4ac) )/(2a)`

⇒
`sinx = (-1 \pm √(1^2-4(2)(-1)) )/(2(2))`

⇒
`sinx = (-1 \pm3)/(4)`

⇒
`sinx = (1)/(2) , sinx =-1`

⇒
`sinx = sin(\pi)/(6) , sinx = sin(3\pi)/(2)`

⇒
`x=(\pi)/(6) , x=(3\pi)/(2)`

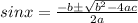
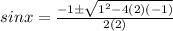
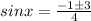
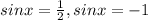
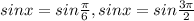
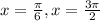
But at
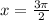`x=(3\pi)/(2)` we have equation undefined as
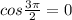`cos(3\pi)/(2)=0` . Hence only solution is :

⇒
`x=(\pi)/(6)`

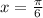
Since ,
`sin(\pi -x)=sinx`

⇒
`x=\pi -(\pi)/(6) = (5\pi)/(6)`

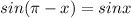
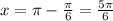
Now , General Solution is given by :

⇒
`x=2k\pi + (\pi)/(6) , x=2k\pi + (5\pi)/(6)`

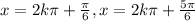
Therefore , Solution to equation
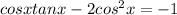`cosxtanx - 2 cos^2 x=-1` for all real values of x is
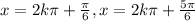`x=2k\pi + (\pi)/(6) , x=2k\pi + (5\pi)/(6)` .