Question

The answer and the work

Answer 1

Explanation:

Let's let
`T` represent the cost of tapes, and
`C` be the cost of CDs.

From the problem statement, we can create the following two equations:

`4T + 2C = 46`

`3T + C = 28`

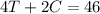
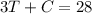
To solve this system of equations, we can solve for
`C` in the second equation and substitute into the first equation to get the value of
`T`:

`3T + C = 28`

`C = 28 - 3T`

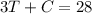
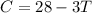
Substitution:

`4T + 2(28 - 3T) = 46`

`4T + 56 - 6T = 46`

`-2T = -10`

`T = 5`

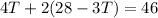
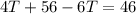
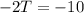
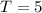
Now that we know the cost of the tapes, we can plug this value into either equation to get the cost of CDs:

`4T + 2C = 46`

`4(5) + 2C = 46`

`20 + 2C = 46`

`2C = 26`

`C = 13`

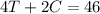
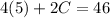
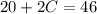
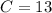
or

`3T + C = 28`

`3(5) + C = 28`

`15 + C = 28`

`C = 13`

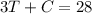
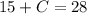
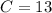
Therefore, the cost of a tape is
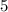`$5` and the cost of a CD is
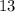`$13`.