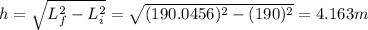Question

Two concrete spans of a 380 m long bridge are

placed end to end so that no room is allowed
for expansion. If the temperature increases by 20◦C, what
is the height to which the spans rise when
they buckle? Assume the thermal coefficient
of expansion is 1.2 × 10^−5(◦C)^−1
Answer in units of m.

Answer 1

4.163 m

Step-by-step explanation:

Since the length of the bridge is

L = 380 m

And the bridge consists of 2 spans, the initial length of each span is

`L_i = (L)/(2)=(380)/(2)=190 m`

Due to the increase in temperature, the length of each span increases according to:

`L_f = L_i(1+ \alpha \Delta T)`

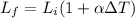
where

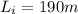`L_i = 190 m` is the initial length of one span

`\alpha =1.2\cdot 10^(-5) ^(\circ)C^(-1)` is the temperature coefficient of thermal expansion

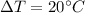`\Delta T=20^(\circ)C` is the increase in temperature

Substituting,

`L_f=(190)(1+(1.2\cdot 10^(-5))(20))=190.0456 m`

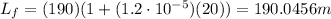
By using Pythagorean's theorem, we can find by how much the height of each span rises due to this thermal expansion (in fact, the new length corresponds to the hypothenuse of a right triangle, in which the base is the original length of the spand, and the rise in heigth is the other side); so we find:

`h=√(L_f^2-L_i^2)=√((190.0456)^2-(190)^2)=4.163 m`