Answer: The expression is undefined when x is 3 or -3
Explanation:
The denominator of a fraction can never be 0 because you cannot divide by 0. So all we have to do is determine the value of x when the denominator is equal to 0.
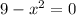
We want
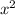 to be positive so divide everything by -1
to be positive so divide everything by -1
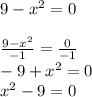
Use difference of two squares (DOTS) to factor
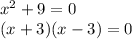
So x cannot be 3 or -3