Binomial distribution formula: P(x) = (n k) p^k * (1 - p)^n - k
a) Probability that four parts are defective = 0.01374
P(4 defective) = (25 4) (0.04)^4 * (0.96)^21
P(4 defective) = 0.01374
b) Probability that at least one part is defective = 0.6396
Find the probability that 0 parts are defective and subtract that probability from 1.
P(0 defective) = (25 0) (0.04)^0 * (0.96)^25
P(0 defective) = 0.3604
1 - 0.3604 = 0.6396
c) Probability that 25 parts are defective = approximately 0
P(25 defective) = (25 25) (0.04)^25 * (0.96)^0
P(25 defective) = approximately 0
d) Probability that at most 1 part is defective = 0.7358
Find the probability that 0 and 1 parts are defective and add them together.
P(0 defective) = 0.3604 (from above)
P(1 defective) = (25 1) (0.04)^1 * (0.96)^24
P(1 defective) = 0.3754
P(at most 1 defective) = 0.3604 + 0.3754 = 0.7358
e) Mean = 1 | Standard Deviation = 0.9798
mean = n * p
mean = 25 * 0.04 = 1
stdev =
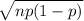
stdev =
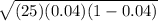 = 0.9798
= 0.9798
Hope this helps!! :)