For the function f(x) =
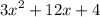
, we need to find the vertex. The vertex is found by first finding
 , and then substituting for
, and then substituting for
 in the function.
in the function.
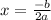
where b is the coefficient of the
 term and a is the coefficient of the
term and a is the coefficient of the
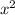 term.
term.
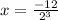

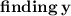
To find

, substitute for

in the given function
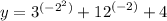

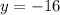
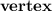
The vertex is
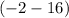
Since the coefficient of the
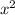
term is positive, we have a minimum.
The minimum is at -16.