Question

Odd numbers starting from 1 were added together. Their total equals to 484. How many numbers were added together?

Answer 1

22 numbers were added together

Explanation:

Notice that the numbers to be added, which are: 1, 3, 5, 7, 9, ..., configure what is called an "arithmetic sequence" where the 'common difference" (d) is "2". "2" is the number we need to add to any element of the sequence in order to generate the next.

Recall as well that the partial sum of "n" terms of an arithmetic sequence (a1, ... an) is;

`S_n=(n\,(a_1+a_n))/(2)`

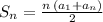
where
`a_1` is the first term of the sequence (in our case "1") and
`a_n` is the nth (last) term to add. We need to find "n" the number of terms of the sequence we need to add in order to obtain 484.

Since we don't know the actual value of the last term to add, we replace it in the equation above by the actual formula to calculate the nth term of an arithmetic sequence:

`a_n=a_1+(n-1)\,d\\a_n=1+(n-1)\,2\\a_n=1+2n-2\\a_n=2n-1`

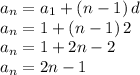
where we have replaced the first term
`a_1` by "1" which is the value of the first term in our case, and "d" (the common difference) by "2" which is the appropriate in our case.

Now we use this expression for
`a_n` in the partial sum equation we need to solve:

`S_n=(n\,(a_1+a_n))/(2) \\484=(n\,(1+(2n-1)))/(2)\\484=(n\,(1+2n-1))/(2)\\484=(n\,(2n))/(2)\\484=n^2`

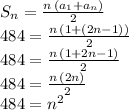
Therefore, to find the value of "n" we calculate the square root of 484

`n^2=484\\n=√(484) \\n=22`

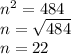
This tells us that there are 22 terms in the sum we need to perform in order to get 484 as the added total.