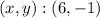Question

Tanisha is thinking of two numbers. The sum of the numbers is 5. If the lesser number is subtracted from the greater number the result is 7. Graph this system of equations to find the two numbers.

x + y = 5
x - y = 7

Answer 1

For this case we have the following system of equations:

`x + y = 5\\x - y = 7`

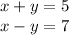
From the first equation we have:

`x = 5-y`

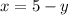
We substitute in the second equation:

`5-y-y = 7\\5-2y = 7`

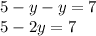
We subtract 5 from both sides of the equation:

`-2y = 7-5\\-2y = 2`

We divide -2 on both sides of the equation:

`y = \frac {2} {- 2}\\y = -1`

So:

`x = 5-y\\x = 5 - (- 1)\\x = 5 + 1\\x = 6`

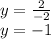
So, the system solution is:
`(x, y) :( 6, -1)`

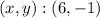
Answer:

See attached image
`(x, y) :( 6, -1)`