Question

Let AB be the line segment beginning at point A(0, 3) and ending at point B(6, -10). Find the point P on the line segment that is of the distance from A to B.

Answer 1

`P=B=(6,-10)`

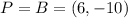
Explanation:

1) Firstly let's place the points in the Cartesian Plane, A is the starting point.

According to the coordinates given:

(Check it out)

2) The distance from A to B, is calculated by:

`d_(AB)=\sqrt{(-10-3)^(2)+(6-0)^2}\cong 14.32\:u`

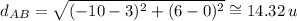
The point P on this line segment AB that is of the distance of 14.32 units is B.

P=B=(6,-10)

Answer 2

Point P = 14.32

Explanation:

Point P represents the distance from point A to point B.

The formula is given as:

`P=\sqrt{(x_(2)-x_(1)) ^(2) + (y_(2)-y_(1)) ^(2)}`

x1 = 0, y1 = 3, x2 = 6, and y2 = -10

`P=\sqrt{(6-0) ^(2) + (-10-3) ^(2)}√(x) \\\\P = \sqrt{6^(2) + (-13)^(2) }= √(36+169) \\\\P = √(205)\\ \\P = 14.3178`

P ≅ 14.32