Question

In a class there are 15 students. 8 of them like playing soccer , 6 of them like swimming , and 2 like both and swimming and playing soccer. How many students do not like either playing soccer or swimming?

Answer 1

3 students

Explanation:

As shown in the Venn diagram, let

x be the number of students who do not like either playing soccer or swimming

U=[Total number of students in the class]

`\implies n(U) = 15`

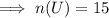
A=[Number of students who like playing soccer]

`\implies n(A) = 8`

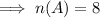
B=[Number of students who like swimming ]

`\implies n(B) = 6`

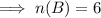
We write mathematically equation in terms of x, for the problem, and solve for x value.

`\implies 6 + 2 + 4 + x = 15`

`\implies 12 + x = 15`

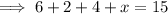
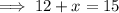
Subtract 12 from both sides.

`\implies 12 - 12 + x = 15 - 12`

`\implies x = 3`

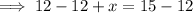
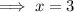
Hence, be the number of students who do not like either playing soccer or swimming is 3.