Answer:
3 students
Explanation:
As shown in the Venn diagram, let
x be the number of students who do not like either playing soccer or swimming
U=[Total number of students in the class]
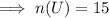
A=[Number of students who like playing soccer]
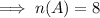
B=[Number of students who like swimming ]
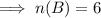
We write mathematically equation in terms of x, for the problem, and solve for x value.

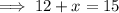
Subtract 12 from both sides.
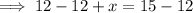
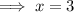
Hence, be the number of students who do not like either playing soccer or swimming is 3.