Answer:
(a) The probability that the members of the committee are chosen from all nationalities
 =0.1212.
=0.1212.
(b)The probability that all nationalities except Italian are represent is 0.04848.
Explanation:
Hypergeometric Distribution:
Let
 ,
,
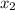 ,
,
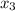 and
and
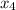 be four given positive integers and let
be four given positive integers and let
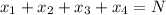 .
.
A random variable X is said to have hypergeometric distribution with parameter
 ,
,
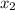 ,
,
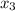 ,
,
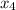 and n.
and n.
The probability mass function
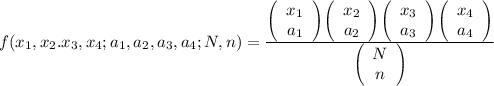
Here

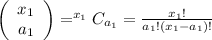
Given that, a foreign club is made of 2 Canadian members, 3 Japanese members, 5 Italian members and 2 Germans members.
 =2,
=2,
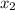 =3,
=3,
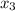 =5 and
=5 and
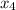 =2.
=2.
A committee is made of 4 member.
N=4
(a)
We need to find out the probability that the members of the committee are chosen from all nationalities.
 =1,
=1,
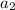 =1,
=1,
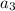 =1 ,
=1 ,
 =1, n=4
=1, n=4
The required probability is
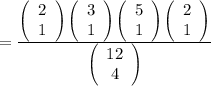


=0.1212
(b)
Now we find out the probability that all nationalities except Italian.
So, we need to find out,
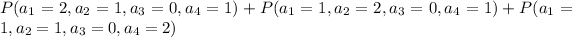

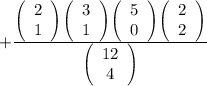
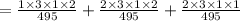
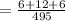
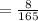
=0.04848
The probability that all nationalities except Italian are represent is 0.04848.