Answer:
The greatest number of displays that can be built using all the boxes are
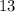
(Using
 blue boxes and
blue boxes and
 yellow boxes for each display).
yellow boxes for each display).
Explanation:
In order to answer the question, the first step is to divide the number of blue boxes and yellow boxes and look for a common ratio ⇒
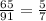
This means that we have a ratio
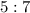 for blue boxes and yellow boxes.
for blue boxes and yellow boxes.
We find that each display will have 5 blue boxes and 7 yellow boxes.
To find the greatest number of displays that can be built we can do the following calculation
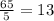
Or
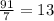
(We can divide the number of blue boxes by its correspond ratio number or the number of yellow boxes by its correspond ratio number)
In each cases the result is 13 displays.
The answer is 13 identical displays