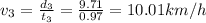1) 18.68 minutes
2) 2.34 %
3) 10.01 km/h
Explanation:
1)
In the first part (swimming part), Surya's velocity is
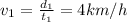
where
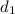 is the length of the swimming part
is the length of the swimming part
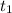 is the time taken to complete the swimming part
is the time taken to complete the swimming part
We can rewrite this equation as
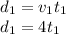 (1)
(1)
In the second part (biking part), Surya's velocity is
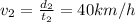
where
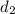 is the length of the biking part
is the length of the biking part
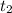 is the time taken to complete the biking part
is the time taken to complete the biking part
We can rewrithe this equation as
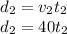 (2)
(2)
The total length of the two segments of the race is:
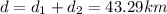 (3)
(3)
And the total time taken to complete them is
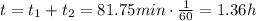 (4)
(4)
Substituting (1) and (2) into (3),
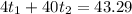 (5)
(5)
From (4), we find:
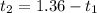
And substituting into (5), we can find t1, the time taken to complete the swimming part of the race:
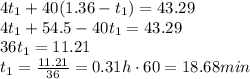
2)
In this part, we are told that the total distance covered by an athlete completing the swim + bycicle + run is
d = 52.95 km
This distance can be written as
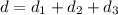
where
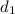 is the length of the swimming part
is the length of the swimming part
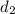 is the length of the biking part
is the length of the biking part
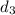 is the length of the running part
is the length of the running part
From the previous part, we can write the length of the swimming part as
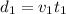
where:
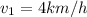 is the velocity in the swimming part
is the velocity in the swimming part
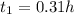 is the time taken for the swimming part
is the time taken for the swimming part
So we have
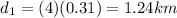
So, the percent of the swimming part over the total is:
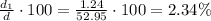
3)
The total time for the entire race must be
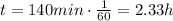
And this total time can be written as
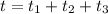
where
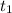 is the time taken to complete the swimming part
is the time taken to complete the swimming part
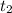 is the time taken to complete the biking part
is the time taken to complete the biking part
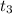 is the time taken to complete the running part
is the time taken to complete the running part
From part 1) we know that
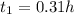
and
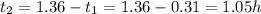
So the time to complete the running part must be
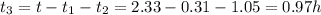
The distance of the last segment is
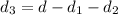
where
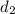 is given by
is given by
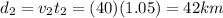
So,
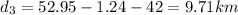
So the average velocity in the 3rd segment is