Question

A solar cooker, really a concave mirror pointed at the Sun, focuses the Sun's rays 13.8 cm in front of the mirror. Part A What is the radius of the spherical surface from which the mirror was made?

Answer 1

From the concept of optics on a curvature of a spherical mirror, the proportion for which the focal length is equivalent to half the radius of curvature is fulfilled. Mathematically this is

`f = (R)/(2)`

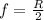
Here,

f = Focal Length

R = Radius

Rearranging to find the radius we have,

`R = 2f`

Replacing with our values,

R = 2(13.8cm)

R = 27.6cm

Therefore the radius of the spherical surface from which the mirror was made is 27.6cm