Answer:
Speed of boat is still water: 16 miles per hour.
Speed of current: 8 miles per hour.
Explanation:
Let x represent speed of boat in still water and y represent speed of current.
Downstream speed would be
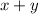 .
.
Upstream speed would be
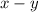 .
.
We have been given that a boat traveled 96 miles downstream and back. The trip downstream took 4 hours.
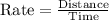
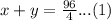
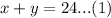
We are also told that the trip back took 12 hours. We can represent this information in an equation as:
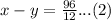
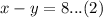
Upon adding equation (1) and equation (2), we will get:
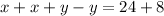
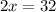
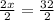
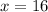
Therefore, the speed of boat in the still water is 16 miles per hour.
Upon substituting
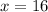 in equation (1), we will get:
in equation (1), we will get:

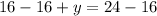
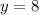
Therefore, the speed of the current is 8 miles per hour.