Question

Given the values of δhfo in kj/mol and so in j/mol k given below, calculate the value of δgo in kj for the reaction at 298 k: c6h12o6(s) + 6 o2(g) => 6 co2(g) + 6h2o(g) δhfo (c6h12o6) = -1,277 δhfo (co2) = -396 δhfo (h2o) = -242 so (c6h12o6(s)) = 218 so (o2(g)) = 206 so (co2(g)) = 211 so (h2o(g)) = 18

Answer 1

Answer : The value of
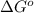`\Delta G^o` for the reaction is, -5386.4 kJ

Explanation :

The given chemical reaction is:

`C_6H_(12)O_6(s)+6O_2(g)\rightarrow 6CO_2(g)+6H_2O(g)`

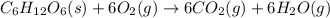
First we have to calculate the entropy of reaction
`(\Delta S^o)`.

`\Delta S^o=S_f_(product)-S_f_(reactant)`

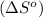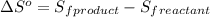
`\Delta S^o=[n_(CO_2(g))* \Delta S^0_((CO_2(g)))+n_(H_2O(g))* \Delta S^0_((H_2O(g)))]-[n_{C_6H_(12)O_6(s)}* \Delta S^0_{(C_6H_(12)O_6(s))}+n_(O_2(g))* \Delta S^0_((O_2(g)))]`

where,

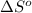`\Delta S^o` = entropy of reaction = ?

n = number of moles

Now put all the given values in this expression, we get:

`\Delta S^o=[6mole* (211J/K.mol)+6mole* (188.7J/K.mol]-[1mole* (218J/K.mol)+6mole* (206J/K.mol]`

`\Delta S^o=944.2J/K`

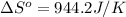
Now we have to calculate the enthalpy of reaction
`(\Delta H^o)`.

`\Delta H^o=H_f_(product)-H_f_(reactant)`

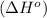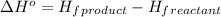
`\Delta H^o=[n_(CO_2(g))* \Delta H^0_((CO_2(g)))+n_(H_2O(g))* \Delta H^0_((H_2O(g)))]-[n_{C_6H_(12)O_6(s)}* \Delta H^0_{(C_6H_(12)O_6(s))}+n_(O_2(g))* \Delta H^0_((O_2(g)))]`

where,

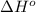`\Delta H^o` = enthalpy of reaction = ?

n = number of moles

Now put all the given values in this expression, we get:

`\Delta H^o=[6mole* (-396kJ/mol)+6mole* (-242kJ/mol]-[1mole* (-1277kJ/mol)+6mole* (0kJ/mol]`

`\Delta H^o=-5105kJ`

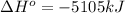
Now we have to calculate the Gibbs free energy.

As we know that,

`\Delta G^o=\Delta H^o-T\Delta S^o`

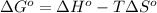
where,

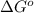`\Delta G^o` = standard Gibbs free energy = ?

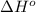`\Delta H^o` = standard enthalpy = -5105 kJ

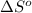`\Delta S^o` = standard entropy = 944.2 J/K = 0.9442 kJ/K

T = temperature of reaction = 298 K

Now put all the given values in the above formula, we get:

`\Delta G^o=(-5105kJ)-(298K* 0.9442kJ/K)`

`\Delta G^o=-5386.4kJ`

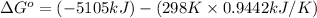
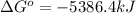
Therefore, the value of
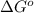`\Delta G^o` for the reaction is, -5386.4 kJ