Question

An equilibrium mixture of 3 kmol of CO, 2.5 kmol of O2, and 8 kmol of N2 is heated to 2600 K at a pressure of 5 atm. Determine the equilibrium composition of the mixture for these conditions.

Answer 1

`x_(CO)=0.0203\\x_(O_2)=0.0926\\x_(CO_2)=0.227\\x_(N_2)=0.660`

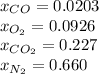
Step-by-step explanation:

Hello,

In this case, we consider the reaction:

`CO(g)+(1)/(2) O_2(g)\rightleftharpoons CO_2`

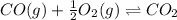
For which the law of mass action is expressed as:

`Kp=(n_(CO_2))/(n_(CO)*n_(O_2)^(1/2)) ((P)/(n_(Tot)) )^(1-1-1/2)`

Whereas the exponents are referred to the stoichiometric coefficients in the chemical reaction. Moreover, in table A-28 (Cengel's thermodynamics) the natural logarithm of the undergoing reaction at 2600 K is 2.801, thus:

`K=exp(2.801)=16.46`

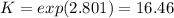
In such a way, in terms of the change
`x` the equilibrium goes:

`16.46=(x)/((3kmol-x)*(2.5kmol-0.5x)^(0.5)) ((5)/(13.5kmol-0.5x) )^(-0.5)`

Hence, solving for
`x`:

`x=2.754kmol`

Thus, the moles at equilibrium:

`n_(CO)=3-2.754=0.246kmol\\n_(O_2)=2.5-0.5(2.754)=1.123kmol\\n_(CO_2)=x=2.754kmol\\n_(N_2)=8kmol`

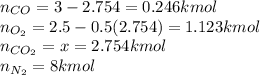
Finally the compositions:

`x_(CO)=(0.246)/(0.246+1.123+2.754+8) =0.0203\\\\x_(O_2)=(1.123)/(0.246+1.123+2.754+8) =0.0926\\\\x_(CO_2)=(2.754)/(0.246+1.123+2.754+8) =0.227\\\\x_(N_2)=(8)/(0.246+1.123+2.754+8) =0.660`

Best regards.