Question

Bara Research Group conducted a survey about church attendance. The survey respondents were asked about their church attendance and asked to indicate their age. Use the sample data to determine whether church attendance is independent of age. Using a level of significance, what is the p-value. Use alpha = 0.05.Church Attendance 20-29 30-39 40-49 50-59Yes 31 63 94 72No 69 87 106 78

Answer 1

The p-value is

- Select your answer -

between .025 and .05

between .05 and .025

between .015 and .045

What is your conclusion?

- Select your answer -

Conclude church attendance is not independent of age.

Conclude church attendance is independent of age.

What conclusion can you draw about church attendance, as individuals grow older?

- Select your answer -

Church attendance increases as individuals grow older.

Church attendance decreases the grow older.

Explanation:

Hello!

There was a survey conducted where the people were asked two questions if they attended church and their age, both answers were recorded, so there are two variables of interest:

X₁: Church attendance, categorized: "Yes" and "No"

X₂: Age of the surveyed person, categorized: "20 to 29", "30 to 39", "40 to 49" and "50 to 59"

The objective is to test if both variables are independent so the hypothesis is:

H₀: Pij= Pi. * P.j ∀ i= 1, 2 and j= 1, 2, 3, 4

H₁: The categorized variables are not independent.

α: 0.05

Tho test this you have to conduct a Chi-Square test of independence, and the statistic is:

`X^2= sum(((O_(ij)-E_(ij))^2)/(E_(ij)) )~~X^2_((r-1)(c-1))`

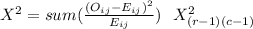
Before calculating the value of the statistic under the null hypothesis you have to calculate all expected frequencies using the following formula:

Eij= (Oi.*O.j)/n

E₁₁= (O₁.*O.₁)/n= (260*100)/600= 43.33

E₁₂= (O₁.*O.₂)/n= (260*150)/600= 65

E₁₃= (O₁.*O.₃)/n= (260*200)/600= 86.67

E₁₄= (O₁.*O.₄)/n= (260*150)/600= 65

E₂₁= (O₂.*O.₁)/n= (340*100)/600= 56.67

E₂₂= (O₂.*O.₂)/n= (340*150)/600= 85

E₂₃= (O₂.*O.₃)/n= (340*200)/600= 113.33

E₂₄= (O₂.*O.₄)/n= (340*150)/600= 85

`X^2= ((31-43.33)^2)/(43.33) +((63-65)^2)/(65) +((94-86.67)^2)/(86.67) +((72-65)^2)/(65) +((69-56.67)^2)/(56.67) +((87-85)^2)/(85) +((106-113.33)^2)/(113.33) +((78-85)^2)/(85)`

`X^2_(H_0)= 8.72`

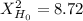
The rejection region for this test is one-tailed to the right with critical value:

`X^2_((r-1)(c-1);1-\alpha )= X^2_(3;0.95)= 7.815`

The p-value for this test is also one-tailed and is

p-value: 0.033255

This p-value is less than the significance level, so the decision is to reject the null hypothesis. At a level of 5%, you can say that church attendance and the age of the people surveyed are not independent.

I hope it helps!