Answer:
A)
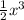
Explanation:
The volume of a triangular prism can be found using the formula
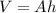 (1)
(1)
where
A is the area of the base
h is the height of the prism
Here, the base is a right triangle; the area of a triangle is

where
b is the base
h' is the height of the triangle
Here, the triangle has the two sides equal, and it is a right triangle, so we have
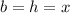
So the area of the base is
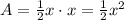
We also know that the height of the prism is equal to the leg length of the base, so
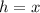
Therefore substituting into (1) we find:
