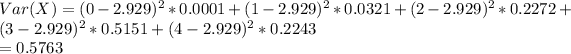Question

Define a random variable x = number of times that owner-occupied units had a water supply stoppage lasting 6 or more hours in the past 3 months and develop a probability distribution for the random variable. (Let x = 4 represent 4 or more times.)

Answer 1

a)

P(0) = 547/14860 = 0.0368

P(1) = 5012/14860 = 0.3373

P(2) = 6100/14860 = 0.4105

P(3) = 2644/14860 = 0.1779

P(4) = 557/14860 = 0.0375

b) Expected Value = 1.842

Variance = 0.7874

c)

P(0) = 23 / 16869 = 0.0001

P(1) = 541 / 16869 = 0.0321

P(2) = 3832 / 16869 = 0.2272

P(3) = 8690 / 16869 = 0.5151

P(4) = 3783 / 16869 = 0.2243

d) Expected Value = 2.929

Variance = 0.5763

e) Owner-occupied houses have more bedrooms in general than renter-occupied houses.

Explanation:

Incomplete Question.

See the complete question: a. Define a random variable x number of bedrooms in renter-occupied houses and develop a probability distribution for the random variable. (Let x 4 represent 4 or more bedrooms.) b. Compute the expected value and variance for the number of bedrooms in renteroccupied houses. c. Define a random variable y number of bedrooms in owner-occupied houses and develop a probability distribution for the random variable. (Let y 4 represent 4 or more bedrooms.) d. Compute the expected value and variance for the number of bedrooms in owneroccupied houses. e. What observations can you make from a comparison of the number of bedrooms in renter-occupied versus owner-occupied homes?

Bedrooms ​ Number ofRenter-Occupied ​Houses Owner-Occupied (1000)

0 547 23

1 5012 541

2 6100 3832

3 2644 8690

4 or more 557 3783

a) Total number of rental

= 547 + 5012 + 6100 + 2644 + 557 = 14860

P(0) = 547/14860 = 0.0368

P(1) = 5012/14860 = 0.3373

P(2) = 6100/14860 = 0.4105

P(3) = 2644/14860 = 0.1779

P(4) = 557/14860 = 0.0375

b) The expected value:

`E(X) = 0 * 0.0368 + 1 * 0.3373 + 2 * 0.4105 + 3 * 0.1779 + 4 * 0.0375\\= 0 + 0.3373 + 0.821 + 0.5337 + 0.15\\= 1.842`

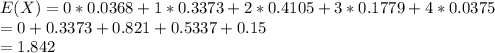
The variance:

`Var(X) = (0-1.842)^(2) * 0.0368 + (1 - 1.842)^(2) * 0.3373 + (2 - 1.842)^2 * 0.4105 + (3-1.842)^2 * 0.1779 + (4 - 1.842)^2 * 0.0375\\= 0.7874`

c) Probabilities for renter-occupied

total number of rental-occupied

= 23 + 541 + 3832 + 8690 + 3783 = 16869

P(0) = 23 / 16869 = 0.0001

P(1) = 541 / 16869 = 0.0321

P(2) = 3832 / 16869 = 0.2272

P(3) = 8690 / 16869 = 0.5151

P(4) = 3783 / 16869 = 0.2243

d) The Expected value:

`E(X) = 0 * 0.0001 + 1 * 0.0321 + 2 * 0.2272 + 3 * 0.5151 + 4 * 0.2243\\= 0 + 0.0321 + 0.4544 + 1.5453 + 0.8972\\= 2.929`

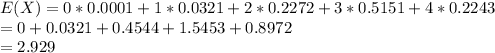
The Variance is:

`Var(X) = (0-2.929)^(2) * 0.0001 + (1 - 2.929)^(2) * 0.0321 + (2 - 2.929)^2 * 0.2272 + (3-2.929)^2 * 0.5151 + (4 - 2.929)^2 * 0.2243\\= 0.5763`

Answer 2

The probability distribution for x is:

`P(x=0)=0.037\\\\P(x=1)=0.339\\\\P(x=2)=0.414\\\\P(x=3)=0.172\\\\P(x=4)=0.038\\\\`

Explanation:

The question is incomplete.

The American Housing Survey reported the following data on the number of times that owner-occupied and renter-occupied units had a water supply stoppage lasting 6 or more hours in the past 3 months.

Number of Houses (1000s)

# Owner Occupied Renter Occupied

0 547 23

1 5,012 541

2 6,110 3,734

3 2,544 8,660

4+ 557 3,784

The sample space of x is [0,1,2,3,4].

We can calculate the probabilities of x as the relative frequency of each value of x.

The total sample size of owner-occupied houses is:

`N=547+5,012+6,110+2,544+557=14,770`

Then, the relative frequencies (equal to the probability) are:

`P(0)=k/n=547/14,770=0.037\\\\P(1)=5,012/14,770=0.339\\\\P(2)=6,110/14,770=0.414\\\\P(3)=2,544/14,770=0.172\\\\P(4)=557/14,770=0.038`