Question

Find the area of the surface in the first octant cut from the cylinder y equals two thirds z Superscript 3 divided by 2 by the planes x equals 3 and y equals 18.

Answer 1

A = 339.531 units^2

Explanation:

Given:-

- The surface of consideration is bounded by the following:

Cylinder :
`Y = (2)/(3)*Z^(3)/(2)`

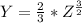
Planes : x = 3 , y = 18

Find:-

Find the area of the surface in the first octant

Solution:-

- It is better to sketch the given curves. Taking (y-z) plane on the sketch paper with x - axis out of the page.

- We see that a surface bounded with 5 faces. We will investigate each face one by one.

Face 1 : This face that lies on the y-z plane defined by the curve of the cylinder and y = 18, and z = x = 0.

• The Area of this face can be calculated by using integral calculus.

`A1 = \int\limits^a_b ({1.5*y)^(2)/(3) } \, dy`

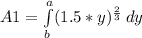
• The limits a,b corresponds to a = y = 18 and b = 0. Evaluate Integral.

`A1 = (1.31037)/(1.6667) *(y^(5)/(3) )\limits _0^1^8 \\\\A1 = (0.786222*18^(5)/(3) ) = 97.19994`

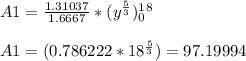
Face 2: This face has the same area as Face 1. This lies on the plane x = 3 defined by the curve and y = 18, z = 0.

A1 = A2 = 97.19994 units^2

Face 3 : This face lies on the plane where y = 18 parallel to x-z plane. Representing a rectangle, defined by plane y = 18 where it intersects the cylinder and z = 0 ... Denoting width of rectangle. While the length is defined by the intersection of planes (y = 18 and x = 3).

• The intersection point of y = 18 and cylinder can be determined by equating both equations and compute the value of z coordinate.

`18 = (2)/(3)*Z^(3)/(2)\\\\Z = 9`

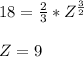
• The area of the Face 3 can then be calculated from the formula:

A3 = Length*Width

A3 = (3)*(9)

A3 = 27 units^2

Face 4 : This face lies on the plane where z = 0 parallel i.e x-y plane. Representing a rectangle, defined by plane y = 18 where it intersects the z = 0 denoting length, while the width is defined by the intersection of planes (x = 3 and z = 0).

The area of Face 4 can be calculated directly from rectangle formula:

A4 = Length*Width

A4 = (3)*(18)

A4 = 54 units^2

Face 5 : This face is curved in nature defined by the cylinder. Which starts from plane x = 0 and limits at x = 3. We will determine the Area of this face by first computing the arc length (L) of the cylinder curve defined by:

`Y = (2)/(3)*Z^(3)/(2)`

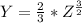
• The arc length formula (L) is given to be:

`L = \int\limits^a_b {} \, ds\\\\ds = \sqrt{1 + ((dy)/(dz))^2 }} dz\\\\(dy)/(dz) = √(z) \\\\ds = \sqrt{1 + (√(z))^2 }} dz\\\\ds = √(1 +z) *dz \\\\L = \int\limits^a_b { √(1 +z)} \, dz\\\\L = (2)/(3)*(1+z)^(^1^.^5^) | \limits_0^9\\\\L = (2)/(3)*[(10.302)^(^1^.^5^) - 1 ] \\\\L = 21.37736`

• We will use the arc length and integrate with respect to x. From x = 0 to x = 3. We have:

A5 = L*( 3 - 0 )

A5 = (21.37736)*(3)

A5 = 64.13208 units^2

- The total surface area of the enclosed body is:

A = A1 + A2 + A3 + A4 + A5

A = 2*(97.1994) + 27 + 54 +64.13208

A = 339.531 units^2