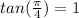Question

Find the exact value of tan pi/4

Answer 1

Explanation:

We'll use the half angle identity for tangent along with the unit circle to find the exact value of tan(π / 4). There are 3 half angle identities for tangent, but I chose this one (just because!):

`tan((\theta)/(2))=(1-cos\theta)/(sin\theta)`

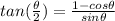
We just need to find the angle to replace theta. It will be

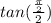`tan(((\pi)/(2) )/(2))` because

`(\pi)/(2) *(1)/(2)=(\pi)/(4)`

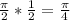
Filling in:

`tan(((\pi)/(2) )/(2))=(1-cos((\pi)/(2)) )/(sin((\pi)/(2)) )`

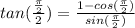
Here's where we'll look to the unit circle to find that the

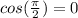`cos((\pi)/(2))=0` and
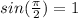`sin((\pi)/(2))=1` so filling those values in gives us:

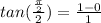`tan(((\pi)/(2) )/(2))=(1-0)/(1)` so the exact value of

`tan((\pi)/(4))=1`

Answer 2

Answer: 1.4×10^-2

Explanation:

Tanpi/4

Pi could be either 22/7 or 3.142

So any of these can be chosen

Pi = 3.142

Pi/4= 3.142/4

=0.7854

Tan 0.7854

= 0.0137

=1.4×10^-2