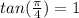Answer:
Explanation:
We'll use the half angle identity for tangent along with the unit circle to find the exact value of tan(π / 4). There are 3 half angle identities for tangent, but I chose this one (just because!):
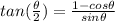
We just need to find the angle to replace theta. It will be
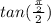 because
because
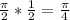
Filling in:
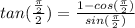
Here's where we'll look to the unit circle to find that the
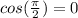 and
and
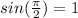 so filling those values in gives us:
so filling those values in gives us:
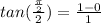 so the exact value of
so the exact value of