Question

Alex is running a recycling business. The weight of collected used Iron in a day is a variable, X, which is normally distributed with mean 203 kg and standard deviation 40 kg. If the cost to recycle each kg of used Iron is $15 and the other cost for running the recycling business per day is $2300, the total expense per day, T, is given by T = 15X + 2300.

(a) Find mean and the standard deviation of T.

(b) There is a 13.8% chance that the total daily expense of the business is more than $K. Find the value of K.

(c) Suppose each kg of collected used Iron can be sold for $35 after the recycling. Find the mean, median and the standard deviation of the daily profit of the business.

(d) Alex can apply for government allowance if there is more than 10% chance that his recycling business has negative profit in a day. Can he apply for the government allowance? Explain your answer with calculation.​

Answer 1

`a.\ \ \ \mu_T=5345, \ \ \sigma_T=600`

`b.\ \ K=$5,995`

`C.\ \ \mu_B=6360, \ median(B)=6360 ,\ \ \sigma_B=800`

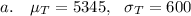
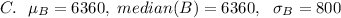
Explanation:

The expense function is expressed as
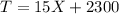`T=15X+2300` where X is the weight of collected iron.

-This function is normal distributed as
`X \sim \mathcal{N}(\mu,\,\sigma^(2))`,
`\mu_x=203, \sigma_x=40`

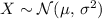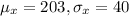
-We use the formula for normal distribution to calculate the mean as:

`=\mu_T=15\mu_x+2300,\ \mu_x=203\\\\=15* 203+2300\\\\=5345`

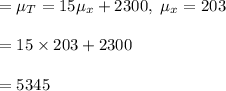
#We then calculate the standard deviation as:

`Var(T)=\sigma_T^2\\\\=15^2* \sigma_x^2\\\\=225* 40^2\\\\=360000\\\sigma_T=√(\sigma_T^2)\\\\\therefore \sigma_T=√(360000)=600`

b. From a above, we know that the cost, T is normally distributed with mean=5345 and standard deviation=600,
`T\sim \mathcal{N}(5345,\,\ 600^2)`

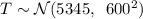
#Given a 13.8% chance that the total daily expense of the business is more than $K, we calculate K as:

`T \sim \mathcal{N}(5345,\,360000)\\\\\\\\Z=(T-5345)/(600) \sim \mathcal{N}(0,\,1)\\=P(T>K)=0.138\\\\\\P(T\leq K)=1-0.138=0.862\\\\P(Z\leq Z^*)=0.8620\\=>Z^*\approx 1.08935\\\\(T^*-5345)/(600)=1.08395\\\\T^*=1.08395* 600+5345\\\\=5995.37\approx5995`

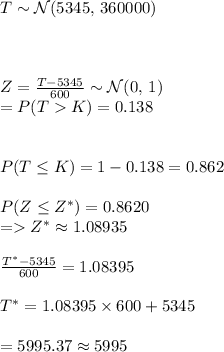
Hence, the value of K is approximately $5995

c. Now given that each kilo or iron collected can be sold for $35, the mean, sd and median of the daily profit is calculated as:

Let B be the profit made:

`B=35X-T\\\\=20X-2300`

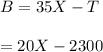
#Mean profit is calculated as:

`\mu_B=20\mu_x-2300, \ \mu_x=203\\\\=20* 203-2300\\\\=6360`

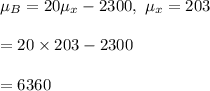
#In a normal distribution:

`mean=mode=median\\\\\\\therefore median(B)=6360`

#The standard deviation is calculated as:

`\sigma_B=√(\sigma_B^2)\\\\=√(20^2\sigma_x^2)\\\\=√(20^2* 40^2)\\\\=800\\\\\therefore \sigma_B=800`

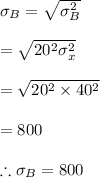
d. A government allowance is applicable if theres 10+% of a negative profit;

`B \sim \mathcal{N}(6360,\,\ 800^(2))\\\\\therefore Z=(B\leq -6360)/(800) \sim \mathcal{N}(0,1)\\\\P(Z\leq Z^*)=0.1, Z^*\approx-1.2816\\\\(B^*-6360)/(800)=-1.2816\\\\B^*=-1.2816* 800+6360\\\\=5334\\\\B=1-(5334.72)/(6360)=0.1612 \ or \ 16.12\%`

16.2%>10%.

Hence, he can apply for government allowance.