Answer:
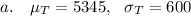
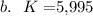
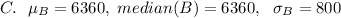
Explanation:
The expense function is expressed as
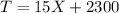 where X is the weight of collected iron.
where X is the weight of collected iron.
-This function is normal distributed as
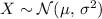 ,
,
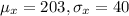
-We use the formula for normal distribution to calculate the mean as:
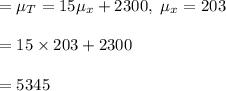
#We then calculate the standard deviation as:
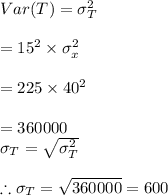
b. From a above, we know that the cost, T is normally distributed with mean=5345 and standard deviation=600,
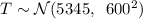
#Given a 13.8% chance that the total daily expense of the business is more than $K, we calculate K as:
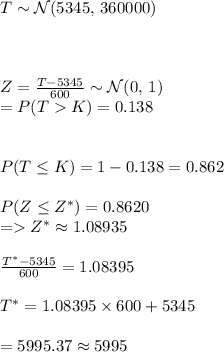
Hence, the value of K is approximately $5995
c. Now given that each kilo or iron collected can be sold for $35, the mean, sd and median of the daily profit is calculated as:
Let B be the profit made:
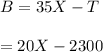
#Mean profit is calculated as:
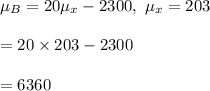
#In a normal distribution:
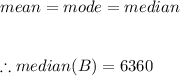
#The standard deviation is calculated as:
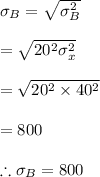
d. A government allowance is applicable if theres 10+% of a negative profit;
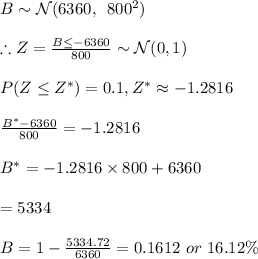
16.2%>10%.
Hence, he can apply for government allowance.